Kalkulator średniej kwadratowej to narzędzie, które pozwala na szybkie i łatwe obliczanie średniej kwadratowej dla Twoich danych. Obliczenie średniej kwadratowej nigdy nie było łatwiejsze, wystarczy wstawić swoje dane odpowiednie pole, aby otrzymać wynik.
Kalkulator średniej kwadratowej
Nasz kalkulator średniej kwadratowej to niezawodne narzędzie do obliczania średniej kwadratowej dla Twoich danych. Kalkulator posiada przejrzysty interfejs z polem tekstowym do wprowadzenia liczb, które należy oddzielić średnikiem. Możliwe jest także ustawienie dokładności wyniku - ilości miejsc po przecinku, zakres od 0 do 8, domyślnie 2 miejsca po przecinku. Wynik pojawia się automatycznie po wprowadzeniu liczb, co pozwala na szybkie i łatwe obliczanie średniej kwadratowej. Skorzystaj z naszego kalkulatora i ciesz się precyzyjnymi i szybkimi wynikami.
Co to jest średnia kwadratowa?
Średnia kwadratowa, jest to pierwiastek z sumy kwadratów wartości podzielonej przez liczbę wartości. Wzór na średnią kwadratową wygląda następująco:
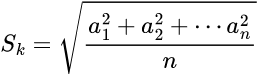
gdzie x1, x2, ...xn to poszczególne wartości z danego zbioru, a n to ich liczba.
Obliczanie średniej kwadratowej
Aby obliczyć średnią kwadratową, należy postępować według następujących kroków:
- Podstawiamy wartości do wzoru i podnosimy każdą wartość do kwadratu.
- Sumujemy te kwadraty.
- Dzielimy sumę przez liczbę wartości.
- Pierwiastkujemy otrzymaną wartość.
- Zastosowanie średniej kwadratowej
Zastosowanie średniej kwadratowej
Średnia kwadratowa jest często stosowana w statystyce, zwłaszcza w analizie danych. Może być również używana w różnych dziedzinach nauki, takich jak fizyka czy chemia. Jest to szczególnie przydatne w przypadku badania zmienności danych, ponieważ pozwala na określenie stopnia rozproszenia danych wokół średniej.
Jednym z przykładów zastosowania średniej kwadratowej jest analiza wariancji w statystyce. Wariancja jest miarą zmienności danych, a średnia kwadratowa jest jej pierwiastkiem kwadratowym. Oznacza to, że wariancja jest miarą zmienności danych wyrażoną w jednostkach danych, a średnia kwadratowa jest tą samą miarą wyrażoną w jednostkach danych kwadratowych.
Średnia kwadratowa jest również często używana w fizyce, zwłaszcza w termodynamice. W termodynamice, średnia kwadratowa prędkości molekuł jest używana do określenia temperatury cieczy lub gazu.
W przypadku nauk ekonomicznych średnia kwadratowa jest używana do obliczania rentowności inwestycji. Rentowność inwestycji jest miarą, jak dobrze inwestycja przynosi zyski w porównaniu do ryzyka.
Podsumowanie
Podsumowując, średnia kwadratowa jest ważnym narzędziem matematycznym, które jest stosowane w wielu dziedzinach nauki i jest przydatne w analizie danych oraz określaniu stopnia rozproszenia danych wokół średniej. Dzięki zrozumieniu tego pojęcia i umiejętności jego obliczania, uczniowie i studenci będą mogli lepiej rozumieć i analizować dane, co przyda im się w przyszłości w różnych dziedzinach nauki i biznesu.