Czy potrzebujesz szybko obliczyć średnią geometryczną? Nasz kalkulator jest tu, aby Ci pomóc! Wprowadź swoje dane, a my obliczymy wynik za Ciebie. Nie musisz tracić czasu na ręczne obliczenia - kalkulator średniej geometrycznej jest prosty w użyciu i pozwoli Ci szybko uzyskać wynik, który jest precyzyjny do wybranej liczby miejsc po przecinku.
Kalkulator średniej geometrycznej
Kalkulator średniej geometrycznej jest prosty w użyciu i pozwoli Ci szybko obliczyć średnią z iloczynu kilku liczb. Aby skorzystać z kalkulatora, wystarczy, że wprowadzisz swoje dane do pola tekstowego, oddzielając je średnikami. Możesz również wybrać, z jaką precyzją chcesz otrzymać wynik, określając liczbę miejsc po przecinku. Każda zmiana w polu tekstowym lub wybór precyzji powoduje automatyczne przeliczenie i wyświetlenie wyniku. Skorzystaj z naszego kalkulatora już dziś i szybko oblicz średnią geometryczną.
Co to jest średnia geometryczna?
Średnia geometryczna to matematyczny wskaźnik średniej, który jest stosowany, gdy chcemy obliczyć średnią arytmetyczną z mnożenia kilku liczb. W innych słowach średnia geometryczna jest to pierwiastek potęgi n z iloczynu n liczb. Jest to często stosowane w przypadku, gdy chcemy uzyskać średnią arytmetyczną dla danych, które są bardzo różne od siebie lub skorelowane liniowo. Może być również używana w wielu dziedzinach, takich jak finansach, statystyce, naukach przyrodniczych i technologii. Należy jednak pamiętać, że średnia geometryczna nie jest dobrze przystosowana do danych, które nie są skorelowane liniowo, oraz nie może być obliczona dla wartości ujemnych.
definicja: średnia geometryczna dwóch lub więcej liczb x1, x2, ..., xn jest równa pierwiastkowi n-tego stopnia z iloczynu tych liczb: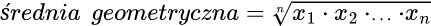
Przykład
Aby obliczyć średnią geometryczną z kilku liczb, wystarczy je pomnożyć razem, a następnie znaleźć pierwiastek z otrzymanego iloczynu, który jest stopnia n.
Na przykład, aby obliczyć średnią geometryczną z liczb 4, 9 i 16, należy wykonać następujące kroki:
- pomnóż razem wszystkie liczby: 4 * 9 * 16 = 576
- znajdź pierwiastek z iloczynu: √576 = 24
W tym przypadku średnia geometryczna wynosi 24.
Zastosowanie średniej geometrycznej w różnych dziedzinach
Średnia geometryczna jest szeroko stosowana w wielu dziedzinach, takich jak finansach, statystyce, naukach przyrodniczych i technologii.
Finanse: Średnia geometryczna jest często stosowana w finansach do obliczania stopy zwrotu z inwestycji. Na przykład, jeśli mamy dane dotyczące stopy zwrotu z 3 różnych inwestycji w ciągu ostatnich 3 lat, możemy obliczyć średnią geometryczną, aby otrzymać średnią roczną stopę zwrotu z tych inwestycji.
Statystyka: Średnia geometryczna jest często stosowana w statystyce do obliczania średniej arytmetycznej dla danych, które są skorelowane liniowo. Na przykład, jeśli mamy dane dotyczące wzrostu ludności w różnych krajach, możemy obliczyć średnią geometryczną, aby otrzymać średni wzrost ludności dla tych krajów.
Nauki przyrodnicze: Średnia geometryczna jest często stosowana w naukach przyrodniczych do obliczania średniej dla wielu wielkości fizycznych, takich jak stężenia substancji chemicznych lub masy ciała. Na przykład, jeśli mamy dane dotyczące stężenia różnych substancji chemicznych w różnych próbkach, możemy obliczyć średnią geometryczną, aby uzyskać średnie stężenie dla tych próbek.
Technologia: Średnia geometryczna jest często stosowana w technologii do obliczania średniej dla wielu parametrów, takich jak moc urządzenia lub jasność ekranu. Na przykład, jeśli mamy dane dotyczące mocy różnych urządzeń, możemy obliczyć średnią geometryczną, aby uzyskać średnią moc dla tych urządzeń.
Średnia geometryczna jest szeroko stosowana w wielu dziedzinach, takich jak finansach, statystyce, naukach przyrodniczych i technologii. Może być używana do obliczania średniej arytmetycznej dla danych, które są bardzo różne od siebie lub skorelowane liniowo. Jest to cenne narzędzie, które należy wziąć pod uwagę podczas analizy danych, chociaż należy pamiętać o jego ograniczeniach, takich jak wrażliwość na wartości ujemne i trudność obliczeniowa.
Wady i zalety stosowania średniej geometrycznej
Średnia geometryczna jest cennym narzędziem matematycznym, które jest stosowane w wielu dziedzinach. Ma jednak kilka ograniczeń, które należy wziąć pod uwagę podczas jej stosowania.
Zalety:
- średnia geometryczna lepiej oddaje rzeczywisty rozkład danych niż średnia arytmetyczna, gdy dane są bardzo różne od siebie;
- średnia geometryczna jest odporna na odstające wartości (outlier'y), co oznacza, że jedna lub kilka odstających wartości nie znacząco wpłynie na ostateczny wynik;
- średnia geometryczna jest często stosowana w statystyce do obliczania średniej dla danych, które są skorelowane liniowo;
Wady:
- Średnia geometryczna jest wrażliwa na wartości ujemne. W przeciwieństwie do średniej arytmetycznej, średnia geometryczna nie może być obliczona dla wartości ujemnych;
- Średnia geometryczna jest trudniejsza do obliczenia niż średnia arytmetyczna, ponieważ wymaga podniesienia wszystkich liczb do potęgi n i obliczenia pierwiastka n-tego stopnia;
- Średnia geometryczna nie jest dobrze przystosowana do danych, które nie są skorelowane liniowo. W takim przypadku lepszym wyborem byłaby średnia harmoniczna lub średnia kwadratowa;
Średnia geometryczna jest cennym narzędziem matematycznym, które ma wiele zalet, takich jak lepsze oddawanie rzeczywistego rozkładu danych i odporność na odstające wartości. Jest również często stosowana w statystyce do obliczania średniej dla danych, które są skorelowane liniowo. Jednakże należy pamiętać o jej ograniczeniach, takich jak wrażliwość na wartości ujemne i trudność obliczeniowa. W przypadku danych, które nie są skorelowane liniowo, lepszym wyborem mogą być inne miary średniej, takie jak średnia harmoniczna lub średnia kwadratowa.